7 Spatial Regression Models: Estimation
\[ \newcommand{\tr}{\mathrm{tr}} \newcommand{\rank}{\mathrm{rank}} \newcommand{\plim}{\operatornamewithlimits{plim}} \newcommand{\diag}{\mathrm{diag}} \newcommand{\bm}[1]{\boldsymbol{\mathbf{#1}}} \newcommand{\Var}{\mathrm{Var}} \newcommand{\Exp}{\mathrm{E}} \newcommand{\Cov}{\mathrm{Cov}} \newcommand\given[1][]{\:#1\vert\:} \newcommand{\irow}[1]{% \begin{pmatrix}#1\end{pmatrix} } \]
This section is strongly based on Sarrias (2023), despite being much less detailed then the original.
Required packages
Session info
R version 4.4.1 (2024-06-14 ucrt)
Platform: x86_64-w64-mingw32/x64
Running under: Windows 11 x64 (build 22631)
Matrix products: default
locale:
[1] LC_COLLATE=English_United Kingdom.utf8
[2] LC_CTYPE=English_United Kingdom.utf8
[3] LC_MONETARY=English_United Kingdom.utf8
[4] LC_NUMERIC=C
[5] LC_TIME=English_United Kingdom.utf8
time zone: Europe/Berlin
tzcode source: internal
attached base packages:
[1] stats graphics grDevices utils datasets methods
[7] base
other attached packages:
[1] viridisLite_0.4.2 tmap_3.3-4 spatialreg_1.3-4
[4] Matrix_1.7-0 spdep_1.3-5 spData_2.3.1
[7] mapview_2.11.2 sf_1.0-16
loaded via a namespace (and not attached):
[1] xfun_0.45 raster_3.6-26 htmlwidgets_1.6.4
[4] lattice_0.22-6 tools_4.4.1 crosstalk_1.2.1
[7] LearnBayes_2.15.1 parallel_4.4.1 stats4_4.4.1
[10] sandwich_3.1-0 proxy_0.4-27 KernSmooth_2.23-24
[13] satellite_1.0.5 RColorBrewer_1.1-3 leaflet_2.2.2
[16] lifecycle_1.0.4 compiler_4.4.1 deldir_2.0-4
[19] munsell_0.5.1 terra_1.7-78 codetools_0.2-20
[22] leafsync_0.1.0 stars_0.6-5 htmltools_0.5.8.1
[25] class_7.3-22 MASS_7.3-60.2 classInt_0.4-10
[28] lwgeom_0.2-14 wk_0.9.1 abind_1.4-5
[31] boot_1.3-30 multcomp_1.4-25 nlme_3.1-164
[34] digest_0.6.35 mvtnorm_1.2-5 splines_4.4.1
[37] fastmap_1.2.0 grid_4.4.1 colorspace_2.1-0
[40] cli_3.6.2 magrittr_2.0.3 base64enc_0.1-3
[43] dichromat_2.0-0.1 XML_3.99-0.16.1 survival_3.6-4
[46] leafem_0.2.3 TH.data_1.1-2 e1071_1.7-14
[49] scales_1.3.0 sp_2.1-4 rmarkdown_2.27
[52] zoo_1.8-12 png_0.1-8 coda_0.19-4.1
[55] evaluate_0.24.0 knitr_1.47 tmaptools_3.1-1
[58] s2_1.1.6 rlang_1.1.4 Rcpp_1.0.12
[61] glue_1.7.0 DBI_1.2.3 rstudioapi_0.16.0
[64] jsonlite_1.8.8 R6_2.5.1 units_0.8-5 Reload data from pervious session
load("_data/msoa2_spatial.RData")Note that most of the spatial model specifications can not be estimated by Least Squares (LS), as using (constrained) LS estimators for models containing a spatially lagged dependent variable or disturbance leads to inconsistent results (Anselin and Bera 1998; Franzese and Hays 2007). However, an extensive amount of econometric literature discusses different estimation methods based on (quasi-) maximum likelihood (Anselin 1988; Lee 2004; Ord 1975) or instrumental variable approaches using generalized methods of moments (Drukker, Egger, and Prucha 2013; Kelejian and Prucha 1998, 2010), in which the endogenous lagged variables can be instrumented by \(q\) higher order lags of the exogenous regressors \(({\bm X}, {\bm W \bm X}, {\bm W^2 \bm X},..., {\bm W^q \bm X})\) (Kelejian and Prucha 1998).
7.1 Simulataneity bias
Remember what is happening when we estimate a spatial auto-regressive model.
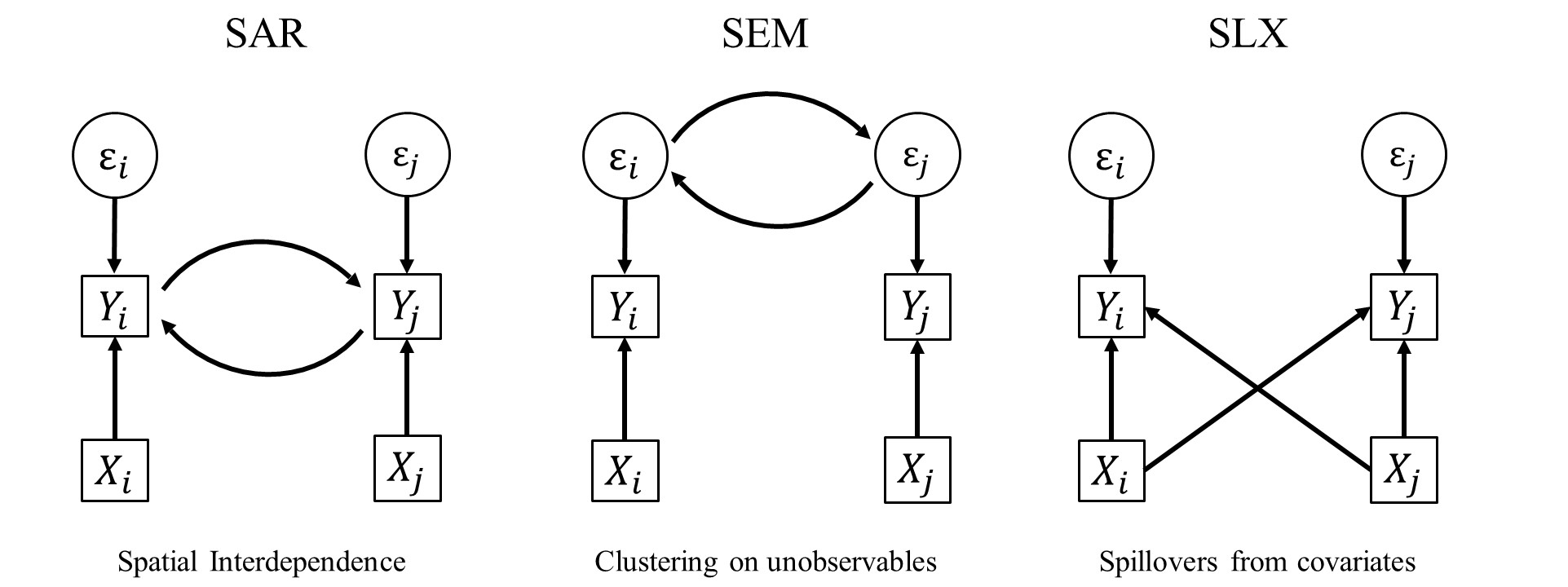
Note the circular process here: My \(X\) influences my \(Y\), which then influences your \(Y\), which then influences my \(Y\) again. We write this as
\[ {\bm y}=\alpha{\bm \iota}+\rho{\bm W}{\bm y}+{\bm X}{\bm \beta}+ {\bm \varepsilon}. \]
If we ignore \({\bm X}{\bm \beta}\) and write the pure auto-regressive term in its reduce form, we get:
\[ \bm y =\left(\bm I_n - \rho\bm W\right)^{-1}\varepsilon, \]
and the spatial lag term is
\[ \bm W \bm y =\bm W\left(\bm I_n - \rho\bm W\right)^{-1}\varepsilon. \]
The OLS estimator for the spatial lag term then is
\[ \hat{\rho}_{OLS} = \left[\underbrace{\left(\bm W\bm y \right)^\intercal}_{(1\times n)}\underbrace{\left(\bm W\bm y \right)}_{(n\times 1)}\right]^{-1}\underbrace{\left(\bm W\bm y \right)^\intercal}_{(1\times n)}\underbrace{\bm y}_{(n\times 1)}. \]
It can then be shown that the OLS estimators equals
\[ \hat{\rho}_{OLS} = \rho + \left[\left(\bm W\bm y \right)^\intercal\left(\bm W\bm y \right)\right]^{-1}\left(\bm W\bm y \right)^\intercal\varepsilon \\ = \rho + \left(\sum_{i = 1}^n \bm y_{Li}^2\right)^{-1}\left(\sum_{i = 1}^{n}\bm y_{Li}\epsilon_i\right), \]
with \(\bm y_{Li}\) defined as the \(i\)th element of the spatial lag operator \(\bm W\bm y = \bm y_L\). It can further be shown that the second part of the equation \(\neq 0\), which demonstrates that OLS gives a biased estimate of \(\rho\) (Franzese and Hays 2007; Sarrias 2023).
Do not estimate spatial lags of the dependent variable in OLS. It will suffer from simultaneity bias.
7.2 Instrumental variable
A potential way of estimating spatial lag /SAR models is 2SLS (Kelejian and Prucha 1998).
We start with our standard model
\[ {\bm y}=\alpha{\bm \iota}+\rho{\bm W}{\bm y}+{\bm X}{\bm \beta}+ {\bm \varepsilon}. \]
As we have seen above, there is a problem of simultaneity: the “covariate” \({\bm W}{\bm y}\) is endogenous. One way of dealing with this endogeneity problem is the Instrumental Variable approach.
So, the question is what are good instruments \(\bm H\) for \({\bm W}{\bm y}\)? As we have specified the mode, we are sure that \({\bm X}\) determines \({\bm y}\). Thus, it must be true that \({\bm W}{\bm X}\) and \({\bm W}^2{\bm X},\ldots, {\bm W}^l{\bm X}\) determines \({\bm W}{\bm y}\).
Note that \({\bm W}^l\) denotes higher orders of \({\bm W}\). So \({\bm W}^2\) are the second order neighbours (neighbours of neighbours), and \({\bm W}^3\) are the third order neighbours (the neighbours of my neighbour’s neighbours), and so on…
We will discuss this in more detail later, but note for now that the reduced form of the SAR always contains a series of higher order neighbours.
\[ ({\bm I_N}-\rho {\bm W})^{-1}\beta_k =({\bm I_N} + \rho{\bm W} + \rho^2{\bm W}^2 + \rho^3{\bm W}^3 + ...)\beta_k = ({\bm I_N} + \sum_{h=1}^\infty \rho^h{\bm W}^h)\beta_k . \]
Thus, Kelejian and Prucha (1998) suggested to use a set of lagged covariates as instruments for \(\bm W \bm Y\):
\[ \bm H = \bm X, \bm W\bm X, \bm W^2\bm X, ... , \bm W^l\bm X, \]
where \(l\) is a pre-defined number for the higher order neighbours included. In practice, \(l\) is usually restricted to \(l=2\).
This has further been developed by, for instance, using a (truncated) power series as instruments (Kelejian, Prucha, and Yuzefovich 2004):
\[ \bm H =\left[\bm X, \bm W\left(\sum_{l = 1}^{\infty}\rho^{l}\bm W^l\right)\bm X \bm\beta\right]. \]
We can estimate this using the pacakge spatialreg with the function stsls(),
mod_1.sls <- stsls(log(med_house_price) ~ log(no2) + log(POPDEN) +
per_mixed + per_asian + per_black + per_other,
data = msoa.spdf,
listw = queens.lw,
robust = TRUE, # heteroskedasticity robust SEs
W2X = TRUE) # Second order neighbours are included as instruments (else only first)
summary(mod_1.sls)
Call:
stsls(formula = log(med_house_price) ~ log(no2) + log(POPDEN) +
per_mixed + per_asian + per_black + per_other, data = msoa.spdf,
listw = queens.lw, robust = TRUE, W2X = TRUE)
Residuals:
Min 1Q Median 3Q Max
-0.5464924 -0.1238002 -0.0052299 0.0989150 1.0793093
Coefficients:
Estimate HC0 std. Error z value Pr(>|z|)
Rho 0.71004211 0.04678235 15.1776 < 2.2e-16
(Intercept) 2.73582523 0.50997823 5.3646 8.113e-08
log(no2) 0.37752751 0.04920257 7.6729 1.688e-14
log(POPDEN) -0.05710992 0.01684036 -3.3913 0.0006957
per_mixed 0.01634307 0.00588488 2.7771 0.0054842
per_asian -0.00205426 0.00045905 -4.4750 7.640e-06
per_black -0.01166456 0.00128557 -9.0734 < 2.2e-16
per_other -0.00280423 0.00332302 -0.8439 0.3987377
Residual variance (sigma squared): 0.035213, (sigma: 0.18765)7.3 Generalized Method of Moments
Generalized Method of Moments (GMM) provides a way of estimating spatial error / SEM models. A motivation for GMM was that Maximum Likelihood was unfeasible for large samples and its consistent could not be shown. Kelejian and Prucha (1999) thus proposed a Moments estimator for SEM.
We start with the model
\[ \begin{split} {\bm y}&=\alpha{\bm \iota}+{\bm X}{\bm \beta}+{\bm u},\\ {\bm u}&=\lambda{\bm W}{\bm u}+{\bm \varepsilon} \end{split} \]
The key issue here is to find a consistent estimator for \(\lambda\). However, we usually do not want to draw inference about \(\lambda\) itself, but only need it to consistently estimate \(\bm \beta\). Kelejian and Prucha (1999) thus treat \(\lambda\) as pure nuisance parameter. They the following moment conditions:
\[ \begin{split} \Exp\left[n^{-1}\varepsilon^\intercal \varepsilon\right] & = \sigma^2, \\ \Exp\left[n^{-1}\varepsilon^\intercal\bm W\bm W\varepsilon\right] & = \frac{\sigma^2}{n}\Exp\left[\tr(\bm W^\intercal\bm W\varepsilon\varepsilon^\intercal) \right],\\ \Exp\left[n^{-1}\varepsilon^\intercal \bm W \varepsilon \right] & = 0, \end{split} \]
which are solved for \(\lambda\), \(\lambda^2\), and \(\sigma^2\) using \(\varepsilon = u - \lambda \bm W u\).
In essence, the GMM works as follows (Sarrias 2023):
First of all obtain a consistent estimate of \(\bm \beta\), say \(\widetilde{\bm \beta}\) using either OLS or non-linear least squares (NLS).
Use this estimate to obtain an estimate of \(\bm u\), say \(\widehat{\bm u}\),
Use \(\widehat{\bm u}\), to estimate \(\lambda\), say \(\widehat{\lambda}\), using
\[ (\widehat{\lambda}_{NLS, n}, \widehat{\sigma}^2_{NLS, N}) = \mathrm{argmin} \left\lbrace \bm \upsilon_n(\lambda, \sigma^2)^\intercal\bm \upsilon_n(\lambda, \sigma^2): \rho \in [-a, a], \sigma^2\in [0, b]\right\rbrace, \]
- Estimate \(\bm \beta\) using Equation
\[ \begin{split} \bm \beta_{FGLS}(\lambda) &=\left[\bm X^\intercal\bm \Omega(\widehat{\lambda})^{-1}\bm X\right]^{-1}\bm X^\intercal\bm \Omega(\widehat{\lambda})^{-1}\bm y.\\ \bm \Omega(\lambda) &= (\bm I - \lambda\bm W)^{-1}(\bm I - \lambda\bm W^\intercal)^{-1} \end{split} \]
For more, see for instance Kelejian and Piras (2017), chapter 2.2.4 or Sarrias (2023).
We can calculate the estimator using GMerrorsar() from spatialreg.
mod_1.gmm <- GMerrorsar(log(med_house_price) ~ log(no2) + log(POPDEN) +
per_mixed + per_asian + per_black + per_other,
data = msoa.spdf,
listw = queens.lw,
se.lambda = TRUE) # Provide standard error for lambda
summary(mod_1.gmm)
Call:
GMerrorsar(formula = log(med_house_price) ~ log(no2) + log(POPDEN) +
per_mixed + per_asian + per_black + per_other, data = msoa.spdf,
listw = queens.lw, se.lambda = TRUE)
Residuals:
Min 1Q Median 3Q Max
-0.8275979 -0.1840855 -0.0096616 0.1610019 1.2270026
Type: GM SAR estimator
Coefficients: (GM standard errors)
Estimate Std. Error z value Pr(>|z|)
(Intercept) 11.07612114 0.26596129 41.6456 < 2.2e-16
log(no2) 0.67758095 0.08620995 7.8597 3.775e-15
log(POPDEN) -0.08006377 0.01464953 -5.4653 4.622e-08
per_mixed -0.01307831 0.00894766 -1.4616 0.1438
per_asian -0.00521983 0.00090937 -5.7400 9.465e-09
per_black -0.01957288 0.00134527 -14.5494 < 2.2e-16
per_other -0.00521695 0.00489760 -1.0652 0.2868
Lambda: 0.69344 (standard error): 0.071248 (z-value): 9.7328
Residual variance (sigma squared): 0.037126, (sigma: 0.19268)
GM argmin sigma squared: 0.037239
Number of observations: 983
Number of parameters estimated: 9 7.4 Maximum likelihood estimation
7.4.1 ML SAR
Maximum Likelihood estimation of spatial models is the most common way of estimation. The procedure to estimate Sar models via ML is based on Ord (1975) and Anselin (1988).
Starting with
\[ \begin{split} \bm y = \rho \bm W\bm y + \bm X\bm \beta + \varepsilon, \\ \varepsilon \sim \mathcal{N}(\bm 0_n , \sigma^2\bm I_n), \end{split} \]
and its reduced form
\[ \begin{split} {\bm y} =({\bm I_N}-\rho {\bm W})^{-1}({\bm X}{\bm \beta}+ {\bm \varepsilon}), \\ {\bm y} =\bm A^{-1}({\bm X}{\bm \beta}+ {\bm \varepsilon}), \end{split} \]
where \(\bm A = ({\bm I_N}-\rho {\bm W})\).
The ML estimator then choses the parameters \(\hat\rho\), \(\hat{\bm \beta}\), and \(\hat\sigma\) to maximize the probability of fitting the observed sample based on the Likelihood function
\[ \begin{split} \mathcal{L} (\bm \theta) &= \log\left| \bm A\right| - \frac{n\log(2\pi)}{2} - \frac{n\log(\sigma^2)}{2} - \frac{1}{2\sigma^2}(\bm A\bm y-\bm X\bm \beta)^\intercal (\bm A\bm y-\bm X\bm \beta) \\ &= \log\left| \bm A\right| - \frac{n\log(2\pi)}{2} - \frac{n\log(\sigma^2)}{2} - \frac{1}{2\sigma^2}\left[\bm y^\intercal \bm A^\intercal\bm A\bm y - 2\left(\bm A\bm y\right)^\intercal\bm X\bm \beta + \bm \beta^\intercal\bm X^\intercal\bm X\bm \beta\right], \end{split} \]
ML estimation of the SAR works as follows Sarrias (2023):
Perform the two auxiliary regression of \(\bm y\) and \(\bm W\bm y\) on \(\bm X\) to obtain the estimators \(\widehat{\bm \beta}_O\) and \(\widehat{\bm \beta}_L\) as in Equation \[ \begin{split} \widehat{\bm \beta}_{ML}(\rho) &= \left(\bm X^\intercal\bm X\right)^{-1}\bm X^\intercal\bm y - \rho\left(\bm X^\intercal\bm X\right)^{-1}\bm X^\intercal\bm W\bm y, \\ &= \widehat{\bm \beta}_O -\rho \widehat{\bm \beta}_L. \end{split} \]
Use \(\widehat{\bm \beta}_O\) and \(\widehat{\bm \beta}_L\) to compute the residuals in Equation \[ \varepsilon_O = \bm y - \bm X\widehat{\bm \beta}_0\,\,\mbox{and} \;\; \varepsilon_L = \bm W\bm y - \bm X\widehat{\bm \beta_L}. \]
By numerical optimization to obtain an estimate of \(\rho\), maximize the concentrated likelihood given in
\[ \ell(\rho)=-\frac{n}{2}-\frac{n}{2}\log(2\pi) - \frac{n}{2}\log\left[\frac{\left(\varepsilon_O - \rho\varepsilon_L\right)^\intercal\left(\varepsilon_O - \rho\varepsilon_L\right)}{n}\right] + \log\left|\bm I_n - \rho\bm W\right|, \]
- Use the estimate of \(\widehat{\rho}\) to plug it back in to the expression for \(\bm \beta\) and \(\sigma^2\)
\[ \begin{split} \widehat{\bm \beta}_{ML}(\rho) = \left(\bm X^\intercal\bm X\right)^{-1}\bm X^\intercal\bm A\bm y \widehat{\sigma}^2_{ML}(\rho) =\\ \frac{\left(\bm A\bm y - \bm X\bm \beta_{ML}\right)^\intercal\left(\bm A\bm y - \bm X\bm \beta_{ML}\right)}{n} \end{split} \]
The evaluation in step 3) can become computation burdensome, as each iteration involves the computation of the \(N \times N\) Jacobian term \(\left|\bm I_n - \rho\bm W\right|\). As shown by Ord (1975), this can be speeded up very heavily by using the log-determinant
\[ \log\left|\bm I_n -\rho\bm W\right|=\sum_{i=1}^n\log(1 - \rho\omega_i). \]
where \(\omega_i\) are the eigenvalues of the weights matrix \(\bm W\). The efficiency gains comes from the fact they also need to be calculated once. However, this requires \(1 - \rho \omega_i \neq 0\) or \(1/\omega_{min} < \rho < 1/\omega_{max}\). This can be ensures by normalising the weights matrix \(\bm W\).
7.4.2 ML SEM
We can also use ML to estimate the spatial error / SEM model of the form
\[ \begin{split} {\bm y}&=\alpha{\bm \iota}+{\bm X}{\bm \beta}+{\bm u},\\ {\bm u}&=\lambda{\bm W}{\bm u}+{\bm \varepsilon}\\ \varepsilon &\sim \mathcal{N}(\bm 0_n , \sigma^2\bm I_n) \end{split} \] Its reduce for is given by
\[ \begin{split} {\bm y}&=\alpha{\bm \iota}+{\bm X}{\bm \beta}+({\bm I_N}-\lambda {\bm W})^{-1}{\bm \varepsilon}.\\ {\bm y}&=\alpha{\bm \iota}+{\bm X}{\bm \beta}+\bm B^{-1}{\bm \varepsilon}. \end{split} \]
where \(\bm B = ({\bm I_N}-\lambda {\bm W})\).
Note that the OLS estimate of the SEM model are unbiased – if there is no omitted variable bias! However, even in that case, they are inefficient if \(\lambda \neq 0\).
The log-likelihood function is given by
\[ \begin{split} \ell(\bm \theta) = - \frac{n}{2}\log(2\pi) - \frac{n}{2}\log(\sigma^2)-\frac{(\bm y - \bm X\bm \beta)^\intercal \bm \Omega(\lambda) (\bm y - \bm X\bm \beta)}{2\sigma^2} + \log\left|\bm I_n - \lambda \bm W\right|, \\ \bm \Omega(\lambda) = \bm B^\intercal \bm B = \left(\bm I_n-\lambda\bm W\right)^\intercal \left(\bm I_n-\lambda\bm W\right) \end{split} \]
Based on Anselin and Bera (1998), the ML estimation of SEM follow the procedure (Sarrias 2023):
Carry out an OLS of \(\bm B\bm X\) on \(\bm B\bm y\); get \(\widehat{\bm \beta}_{OLS}\)
Compute initial set of residuals \(\widehat{\epsilon}_{OLS} = \bm B\bm y - \bm B\bm X\widehat{\bm \beta}_{OLS}\)
Given \(\widehat{\epsilon}_{OLS}\), find \(\widehat{\lambda}\) that maximizes the concentrated likelihood
\[ \ell(\lambda)= \mbox{const} + \frac{n}{2}\log\left[\frac{1}{n}\widehat{\bm \varepsilon}^\intercal\bm B^\intercal\bm B \widehat{\bm \varepsilon}\right] + \log\left|\bm B\right|. \]
If the convergence criterion is met, proceed, otherwise repeat steps 1, 2 and 3.
Given \(\widehat{\lambda}\), estimate \(\widehat{\bm \beta}(\lambda)\) by GLS and obtain a new vector of residuals, \(\widehat{\bm \varepsilon}(\lambda)\)
Given \(\widehat{\bm \varepsilon}(\lambda)\) and \(\widehat{\lambda}\), estimate \(\widehat{\sigma}(\lambda)\).
The package spatialreg Pebesma and Bivand (2023) provides a series of functions to calculate the ML estimator for all spatial models we have considered.
Table from Pebesma and Bivand (2023):
| model | model name | maximum likelihood estimation function |
|---|---|---|
| SEM | spatial error | errorsarlm(..., Durbin=FALSE) |
| SEM | spatial error | spautolm(..., family="SAR") |
| SDEM | spatial Durbin error | errorsarlm(..., Durbin=TRUE) |
| SLM | spatial lag | lagsarlm(..., Durbin=FALSE) |
| SDM | spatial Durbin | lagsarlm(..., Durbin=TRUE) |
| SAC | spatial autoregressive combined | sacsarlm(..., Durbin=FALSE) |
| GNM | general nested | sacsarlm(..., Durbin=TRUE) |
ML SAR
mod_1.sar <- lagsarlm(log(med_house_price) ~ log(no2) + log(POPDEN) +
per_mixed + per_asian + per_black + per_other,
data = msoa.spdf,
listw = queens.lw,
Durbin = FALSE) # we could here extend to SDM
summary(mod_1.sar)
Call:
lagsarlm(formula = log(med_house_price) ~ log(no2) + log(POPDEN) +
per_mixed + per_asian + per_black + per_other, data = msoa.spdf,
listw = queens.lw, Durbin = FALSE)
Residuals:
Min 1Q Median 3Q Max
-0.5281789 -0.1220524 -0.0099245 0.0992203 1.0936745
Type: lag
Coefficients: (asymptotic standard errors)
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.17383180 0.29041604 10.9286 < 2.2e-16
log(no2) 0.39705423 0.04452880 8.9168 < 2.2e-16
log(POPDEN) -0.05583014 0.01242876 -4.4920 7.055e-06
per_mixed 0.01851577 0.00579832 3.1933 0.001407
per_asian -0.00228346 0.00045876 -4.9775 6.442e-07
per_black -0.01263650 0.00100282 -12.6009 < 2.2e-16
per_other -0.00161419 0.00289082 -0.5584 0.576582
Rho: 0.66976, LR test value: 473.23, p-value: < 2.22e-16
Asymptotic standard error: 0.025311
z-value: 26.461, p-value: < 2.22e-16
Wald statistic: 700.19, p-value: < 2.22e-16
Log likelihood: 196.7203 for lag model
ML residual variance (sigma squared): 0.035402, (sigma: 0.18815)
Number of observations: 983
Number of parameters estimated: 9
AIC: -375.44, (AIC for lm: 95.786)
LM test for residual autocorrelation
test value: 8.609, p-value: 0.0033451ML SEM
mod_1.sem <- errorsarlm(log(med_house_price) ~ log(no2) + log(POPDEN) +
per_mixed + per_asian + per_black + per_other,
data = msoa.spdf,
listw = queens.lw,
Durbin = FALSE) # we could here extend to SDEM
summary(mod_1.sem)
Call:
errorsarlm(formula = log(med_house_price) ~ log(no2) + log(POPDEN) +
per_mixed + per_asian + per_black + per_other, data = msoa.spdf,
listw = queens.lw, Durbin = FALSE)
Residuals:
Min 1Q Median 3Q Max
-0.581785 -0.105218 -0.012758 0.094430 0.913425
Type: error
Coefficients: (asymptotic standard errors)
Estimate Std. Error z value Pr(>|z|)
(Intercept) 12.92801104 0.35239139 36.6865 < 2.2e-16
log(no2) 0.15735296 0.10880727 1.4462 0.1481317
log(POPDEN) -0.08316270 0.01254315 -6.6301 3.354e-11
per_mixed -0.03377962 0.00811054 -4.1649 3.115e-05
per_asian -0.00413115 0.00096849 -4.2656 1.994e-05
per_black -0.01653816 0.00126741 -13.0488 < 2.2e-16
per_other -0.01693012 0.00462999 -3.6566 0.0002556
Lambda: 0.88605, LR test value: 623.55, p-value: < 2.22e-16
Asymptotic standard error: 0.015803
z-value: 56.068, p-value: < 2.22e-16
Wald statistic: 3143.6, p-value: < 2.22e-16
Log likelihood: 271.8839 for error model
ML residual variance (sigma squared): 0.026911, (sigma: 0.16405)
Number of observations: 983
Number of parameters estimated: 9
AIC: -525.77, (AIC for lm: 95.786)