Part 2: Analysing spatial data
Tobias Rüttenauer
June 19, 2021
Required packages
pkgs <- c("sf", "mapview", "spdep", "spatialreg", "tmap", "GWmodel", "viridisLite") # note: load spdep first, then spatialreg
lapply(pkgs, require, character.only = TRUE)Session info
sessionInfo()## R version 4.1.0 (2021-05-18)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
## Running under: Windows 10 x64 (build 19042)
##
## Matrix products: default
##
## locale:
## [1] LC_COLLATE=English_United Kingdom.1252
## [2] LC_CTYPE=English_United Kingdom.1252
## [3] LC_MONETARY=English_United Kingdom.1252
## [4] LC_NUMERIC=C
## [5] LC_TIME=English_United Kingdom.1252
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] viridisLite_0.4.0 GWmodel_2.2-6 Rcpp_1.0.6
## [4] robustbase_0.93-8 maptools_1.1-1 tmap_3.3-1
## [7] spatialreg_1.1-8 Matrix_1.3-3 spdep_1.1-8
## [10] spData_0.3.8 sp_1.4-5 dplyr_1.0.6
## [13] rnaturalearth_0.1.0 nngeo_0.4.3 mapview_2.10.0
## [16] gstat_2.0-7 sf_1.0-0
##
## loaded via a namespace (and not attached):
## [1] nlme_3.1-152 xts_0.12.1 satellite_1.0.2
## [4] webshot_0.5.2 gmodels_2.18.1 RColorBrewer_1.1-2
## [7] tools_4.1.0 bslib_0.2.5.1 utf8_1.2.1
## [10] rgdal_1.5-23 R6_2.5.0 KernSmooth_2.23-20
## [13] rgeos_0.5-5 DBI_1.1.1 colorspace_2.0-1
## [16] raster_3.4-10 rnaturalearthdata_0.1.0 tidyselect_1.1.1
## [19] leaflet_2.0.4.1 compiler_4.1.0 leafem_0.1.6
## [22] expm_0.999-6 sass_0.4.0 scales_1.1.1
## [25] DEoptimR_1.0-9 classInt_0.4-3 proxy_0.4-26
## [28] systemfonts_1.0.2 stringr_1.4.0 digest_0.6.27
## [31] foreign_0.8-81 rmarkdown_2.8 svglite_2.0.0
## [34] dichromat_2.0-0 base64enc_0.1-3 pkgconfig_2.0.3
## [37] htmltools_0.5.1.1 highr_0.9 htmlwidgets_1.5.3
## [40] rlang_0.4.11 FNN_1.1.3 jquerylib_0.1.4
## [43] farver_2.1.0 generics_0.1.0 zoo_1.8-9
## [46] jsonlite_1.7.2 gtools_3.9.2 crosstalk_1.1.1
## [49] magrittr_2.0.1 munsell_0.5.0 fansi_0.5.0
## [52] abind_1.4-5 lifecycle_1.0.0 leafsync_0.1.0
## [55] stringi_1.6.2 yaml_2.2.1 MASS_7.3-54
## [58] tmaptools_3.1-1 grid_4.1.0 parallel_4.1.0
## [61] gdata_2.18.0 crayon_1.4.1 deldir_0.2-10
## [64] lattice_0.20-44 stars_0.5-3 splines_4.1.0
## [67] leafpop_0.1.0 knitr_1.33 pillar_1.6.1
## [70] uuid_0.1-4 boot_1.3-28 spacetime_1.2-5
## [73] codetools_0.2-18 stats4_4.1.0 LearnBayes_2.15.1
## [76] XML_3.99-0.6 glue_1.4.2 evaluate_0.14
## [79] leaflet.providers_1.9.0 png_0.1-7 vctrs_0.3.8
## [82] purrr_0.3.4 assertthat_0.2.1 xfun_0.23
## [85] lwgeom_0.2-6 e1071_1.7-7 coda_0.19-4
## [88] class_7.3-19 tibble_3.1.2 intervals_0.15.2
## [91] units_0.7-2 ellipsis_0.3.2 brew_1.0-6Load spatial data
See previous file.
load("_data/msoa_spatial.RData")Spatial interdependence
We can not only use coordinates and geo-spatial information to connect different data sources, we can also explicitly model spatial (inter)depence in the analysis of our data. In many instance, accounting for spatial dependence might even be necessary to avoid biased point estimates and standard errors, as observations are often not independent and identically distributed. ‘Everything is related to everything else, but near things are more related than distant things’ (Tobler 1970).
However, even if we would receive unbiased estimates with conventional methods, using the spatial information of the data can help us detect specific patterns and spatial relations.
\({\boldsymbol{\mathbf{W}}}\): Connectivity between units
To analyse spatial relations, we first need to define some sort of connectivity between units (e.g. similar to network analysis). There is an ongoing debate about the importance of spatial weights for spatial econometrics and about the right way to specify weights matrices Neumayer and Plümper (2016). The following graph shows some possible options in how to define connectivity between units.
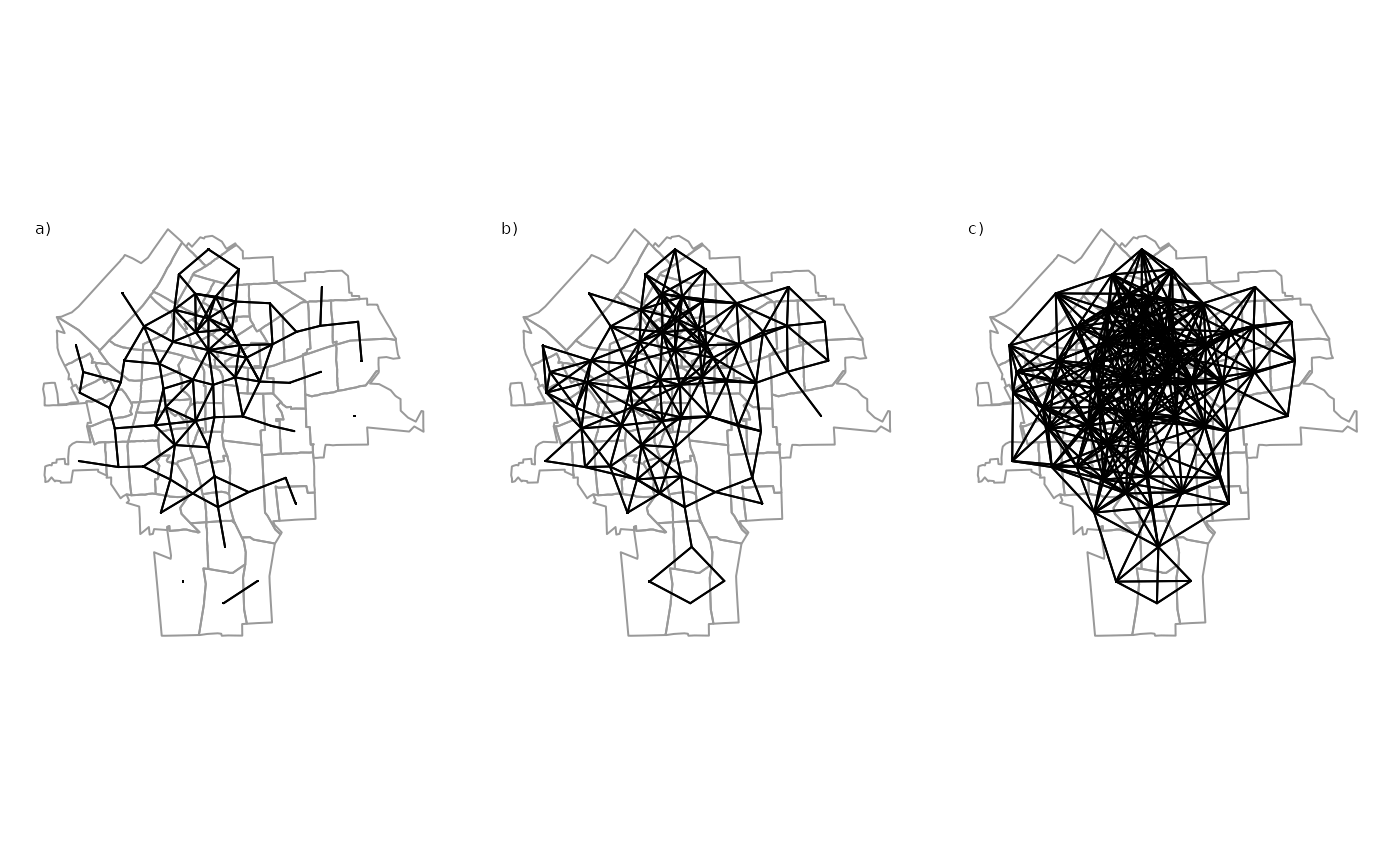
Figure: Spatial data linkage, Source: Bivand, Pebesma, and Gómez-Rubio (2008)
In spatial econometrics, the spatial connectivity (as shown above) is usually represented by a spatial weights matrix \({\boldsymbol{\mathbf{W}}}\): \[ \begin{equation} \boldsymbol{\mathbf{W}} = \begin{bmatrix} w_{11} & w_{12} & \dots & w_{1n} \\ w_{21} & w_{22} & \dots & w_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n1} & w_{n2} & \dots & w_{nn} \end{bmatrix} \end{equation} \] The spatial weights matrix \(\boldsymbol{\mathbf{W}}\) is an \(N \times N\) dimensional matrix with elements \(w_{ij}\) specifying the relation or connectivity between each pair of units \(i\) and \(j\).
Note: The diagonal elements \(w_{i,i}= w_{1,1}, w_{2,2}, \dots, w_{n,n}\) of \(\boldsymbol{\mathbf{W}}\) are always zero. No unit is a neighbour of itself.
Contiguity weights
A very common type of spatial weights. Binary specification, taking the value 1 for neighbouring units (queens: sharing a common edge; rook: sharing a common border), and 0 otherwise.
Contiguity weights \(w_{i,j} =\)
1 if \(i\) and \(j\) neighbours
0
\[ \begin{equation} \boldsymbol{\mathbf{W}} = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix} \nonumber \end{equation} \]
Sparse matrices
Problem of `island’ (units without neighbours)
Lets create a contiguity weights matrix (Queens neighbours) for the London MSOAs: we create a neighbours list (nb) using poly2nb(), which is an efficient way of storing \({\boldsymbol{\mathbf{W}}}\).
# Contiguity (Queens) neighbours weights
queens.nb <- poly2nb(msoa.spdf,
queen = TRUE,
snap = 1) # we consider points in 1m distance as 'touching'
summary(queens.nb)## Neighbour list object:
## Number of regions: 983
## Number of nonzero links: 5620
## Percentage nonzero weights: 0.5816065
## Average number of links: 5.717192
## Link number distribution:
##
## 2 3 4 5 6 7 8 9 10 11 12 13
## 9 40 132 268 279 159 63 19 6 5 2 1
## 9 least connected regions:
## 160 270 475 490 597 729 755 778 861 with 2 links
## 1 most connected region:
## 946 with 13 links# Lets plot that
plot(st_geometry(msoa.spdf), border = "grey60")
plot(queens.nb, st_centroid(st_geometry(msoa.spdf)),
add = TRUE, pch = 19, cex = 0.6)
# We can also transform this into a matrix W
W <- nb2mat(queens.nb, style = "B")
print(W[1:10, 1:10])## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## 1 0 0 0 0 0 0 0 0 0 0
## 2 0 0 1 0 0 0 0 0 0 0
## 3 0 1 0 0 1 0 0 0 0 0
## 4 0 0 0 0 0 1 0 0 0 1
## 5 0 0 1 0 0 1 1 0 0 0
## 6 0 0 0 1 1 0 1 0 1 1
## 7 0 0 0 0 1 1 0 1 1 0
## 8 0 0 0 0 0 0 1 0 0 0
## 9 0 0 0 0 0 1 1 0 0 1
## 10 0 0 0 1 0 1 0 0 1 0Distance based weights
Another common type uses the distance \(d_{ij}\) between each unit \(i\) and \(j\).
- Inverse distance weights \(w_{i,j} = \frac{1}{d_{ij}^\alpha}\), where \(\alpha\) define the strength of the spatial decay.
\[ \begin{equation} \boldsymbol{\mathbf{W}} = \begin{bmatrix} 0 & \frac{1}{d_{ij}^\alpha} & \frac{1}{d_{ij}^\alpha} \\ \frac{1}{d_{ij}^\alpha} & 0 & \frac{1}{d_{ij}^\alpha} \\ \frac{1}{d_{ij}^\alpha} & \frac{1}{d_{ij}^\alpha} & 0 \end{bmatrix} \nonumber \end{equation} \]
Dense matrices
Specifying thresholds may be useful (to get rid of very small non-zero weights)
For now, we will just specify a neighbours list with a distance threshold of 3km using dnearneigh(). An alternative would be k nearest neighbours using knearneigh(). We will do the inverse weighting later.
# Crease centroids
coords <- st_geometry(st_centroid(msoa.spdf))## Warning in st_centroid.sf(msoa.spdf): st_centroid assumes attributes are
## constant over geometries of x# Neighbours within 3km distance
dist_3.nb <- dnearneigh(coords, d1 = 0, d2 = 3000)
summary(dist_3.nb)## Neighbour list object:
## Number of regions: 983
## Number of nonzero links: 22086
## Percentage nonzero weights: 2.285652
## Average number of links: 22.46796
## Link number distribution:
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
## 4 3 7 13 11 14 14 17 26 22 26 30 33 34 46 34 59 43 38 30 25 19 22 15 21 14
## 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
## 23 17 17 23 28 19 26 24 29 24 27 25 22 18 8 10 12 5 3 2 1
## 4 least connected regions:
## 158 160 463 959 with 1 link
## 1 most connected region:
## 545 with 47 links# Lets plot that
plot(st_geometry(msoa.spdf), border = "grey60")
plot(dist_3.nb, coords,
add = TRUE, pch = 19, cex = 0.6)
Normalization of \({\boldsymbol{\mathbf{W}}}\)
Normalizing ensures that the parameter space of the spatial multiplier is restricted to \(-1 < \rho > 1\), and the multiplier matrix is non-singular. Again, how to normalize a weights matrix is subject of debate (LeSage and Pace 2014; Neumayer and Plümper 2016).
Normalizing your weights matrix is always a good idea. Otherwise, the spatial parameters might blow up – if you can estimate the model at all.
Row-normalization
Row-normalization divides each non-zero weight by the sum of all weights of unit \(i\), which is the sum of the row.
\[ \frac{w_{ij}}{\sum_j^n w_{ij}} \]
With contiguity weights, spatial lags contain average value of neighbours
Proportions between units (distance based) get lost
Can induce asymmetries: \(w_{ij} \neq w_{ji}\)
For instance, we can use row-normalization for the Queens neighbours created above, and create a neighbours list with spatial weights
queens.lw <- nb2listw(queens.nb,
style = "W") # W ist row-normalization
summary(queens.lw)## Characteristics of weights list object:
## Neighbour list object:
## Number of regions: 983
## Number of nonzero links: 5620
## Percentage nonzero weights: 0.5816065
## Average number of links: 5.717192
## Link number distribution:
##
## 2 3 4 5 6 7 8 9 10 11 12 13
## 9 40 132 268 279 159 63 19 6 5 2 1
## 9 least connected regions:
## 160 270 475 490 597 729 755 778 861 with 2 links
## 1 most connected region:
## 946 with 13 links
##
## Weights style: W
## Weights constants summary:
## n nn S0 S1 S2
## W 983 966289 983 356.6902 4018.36Maximum eigenvalues normalization
Maximum eigenvalues normalization divides each non-zero weight by the overall maximum eigenvalue \(\lambda_{max}\). Each element of \(\boldsymbol{\mathbf{W}}\) is divided by the same scalar parameter.
\[ \frac{\boldsymbol{\mathbf{W}}}{\lambda_{max}} \]
Interpretation may become more complicated
Keeps proportions of connectivity strengths across units (relevant esp. for distance based \(\boldsymbol{\mathbf{W}}\))
We use eigenvalue normalization for the inverse distance neighbours. We use nb2listwdist() to create weight inverse distance based weights and normalize in one step.
idw.lw <- nb2listwdist(dist_3.nb,
x = coords, # needed for idw
type = "idw", # inverse distance weighting
alpha = 1, # the decay parameter for distance weighting
style = "minmax") # for eigenvalue normalization
summary(idw.lw)## Characteristics of weights list object:
## Neighbour list object:
## Number of regions: 983
## Number of nonzero links: 22086
## Percentage nonzero weights: 2.285652
## Average number of links: 22.46796
## Link number distribution:
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
## 4 3 7 13 11 14 14 17 26 22 26 30 33 34 46 34 59 43 38 30 25 19 22 15 21 14
## 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
## 23 17 17 23 28 19 26 24 29 24 27 25 22 18 8 10 12 5 3 2 1
## 4 least connected regions:
## 158 160 463 959 with 1 link
## 1 most connected region:
## 545 with 47 links
##
## Weights style: minmax
## Weights constants summary:
## n nn S0 S1 S2
## minmax 983 966289 463.6269 23.92505 1117.636Islands / missings
In practice, we often have a problem with islands. If we use contiguity based or distance based neighbour definitions, some units may end up with empty neighbours sets: they just do not touch any other unit and do not have a neighbour within a specific distance. This however creates a problem: what is the value in the neighbouring units?
The zero.policy option in spdep allows to proceed with empty neighbours sets. However, many further functions may run into problems and return errors. It often makes sense to either drop islands, to choose weights which always have neighbours (e.g. k nearest), or impute empty neighbours sets by using the nearest neighbours.
Spatial Autocorrelation
If spatially close observations are more likely to exhibit similar values, we cannot handle observations as if they were independent.
\[ \mathrm{E}(\varepsilon_i\varepsilon_j)\neq \mathrm{E}(\varepsilon_i)\mathrm{E}(\varepsilon_j) = 0 \]
This violates a basic assumption of the conventional OLS model. In consequence, ignoring spatial dependence can lead to
biased inferential statistics
biased point estimates (depending on the DGP)
Visualization
There is one very easy and intuitive way of detecting spatial autocorrelation: Just look at the map. We do so by using tmap for plotting the housing values.
mp1 <- tm_shape(msoa.spdf) +
tm_fill(col = "Value",
#style = "cont",
style = "fisher", n = 8,
title = "Median",
palette = viridis(n = 8, direction = -1, option = "C"),
legend.hist = TRUE) +
tm_borders(col = "black", lwd = 1) +
tm_layout(legend.frame = TRUE, legend.bg.color = TRUE,
#legend.position = c("right", "bottom"),
legend.outside = TRUE,
main.title = "House values 2017",
main.title.position = "center",
title.snap.to.legend = TRUE)
mp1 
## [1] "#F0F921" "#FEBC2A" "#F48849" "#DB5C68" "#B93289" "#8B0AA5" "#5402A3"
## [8] "#0D0887"Moran’s I
Global Moran’s I test statistic: \[ \begin{equation} \boldsymbol{\mathbf{I}} = \frac{N}{S_0} \frac{\sum_i\sum_j w_{ij}(y_i-\bar{y})(y_j-\bar{y})} {\sum_i (y_i-\bar{y})}, \text{where } S_0 = \sum_{i=1}^N\sum_{j=1}^N w_{ij} \end{equation} \]
Relation of the deviation from the mean value between unit \(i\) and neighbours of unit \(i\). Basically, this measures correlation between neighbouring values.
Negative values: negative autocorrelation
Around zero: no autocorrelation
Positive values: positive autocorrelation
# Global Morans I test of housing values based on contiguity weights
moran.test(msoa.spdf$Value, listw = queens.lw, alternative = "two.sided")##
## Moran I test under randomisation
##
## data: msoa.spdf$Value
## weights: queens.lw
##
## Moran I statistic standard deviate = 37.238, p-value < 2.2e-16
## alternative hypothesis: two.sided
## sample estimates:
## Moran I statistic Expectation Variance
## 0.7068094990 -0.0010183299 0.0003613048# Global Morans I test of housing values based on idw
moran.test(msoa.spdf$Value, listw = idw.lw, alternative = "two.sided")##
## Moran I test under randomisation
##
## data: msoa.spdf$Value
## weights: idw.lw
##
## Moran I statistic standard deviate = 70.475, p-value < 2.2e-16
## alternative hypothesis: two.sided
## sample estimates:
## Moran I statistic Expectation Variance
## 0.7260392810 -0.0010183299 0.0001064319Spatial Regression Models
There are various techniques to model spatial dependence and spatial processes (LeSage and Pace 2009). Here, we will just cover a few of the most common techniques / econometric models. One advantage of the most basic spatial model (SLX) is that this method can easily be incorporated in a variety of other methodologies, such as machine learning approaches. Halleck Vega and Elhorst (2015), LeSage (2014), and Rüttenauer (2019) provide article-length introductions.
There are three basic ways of incorporating spatial dependece.
Spatial Error Model (SEM)
- Clustering on Unobservables
\[ \begin{equation} \begin{split} {\boldsymbol{\mathbf{y}}}&=\alpha{\boldsymbol{\mathbf{\iota}}}+{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\beta}}}+{\boldsymbol{\mathbf{u}}},\\ {\boldsymbol{\mathbf{u}}}&=\lambda{\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{u}}}+{\boldsymbol{\mathbf{\varepsilon}}} \end{split} \end{equation} \]
Spatial Autoregressive Model (SAR)
- Interdependence
\[ \begin{equation} {\boldsymbol{\mathbf{y}}}=\alpha{\boldsymbol{\mathbf{\iota}}}+\rho{\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{y}}}+{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\beta}}}+ {\boldsymbol{\mathbf{\varepsilon}}} \end{equation} \]
Spatially lagged X Model (SLX)
- Clustering on Spillovers in Covariates
\[
\begin{equation}
{\boldsymbol{\mathbf{y}}}=\alpha{\boldsymbol{\mathbf{\iota}}}+{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\beta}}}+{\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\theta}}}+ {\boldsymbol{\mathbf{\varepsilon}}}
\end{equation}
\]
Moreover, there are models combining two sets of the above specifications.
Spatial Durbin Model (SDM)
\[ \begin{equation} {\boldsymbol{\mathbf{y}}}=\alpha{\boldsymbol{\mathbf{\iota}}}+\rho{\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{y}}}+{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\beta}}}+{\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\theta}}}+ {\boldsymbol{\mathbf{\varepsilon}}} \end{equation} \]
Spatial Durbin Error Model (SDEM)
\[ \begin{equation} \begin{split} {\boldsymbol{\mathbf{y}}}&=\alpha{\boldsymbol{\mathbf{\iota}}}+{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\beta}}}+{\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\theta}}}+ {\boldsymbol{\mathbf{u}}},\\ {\boldsymbol{\mathbf{u}}}&=\lambda{\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{u}}}+{\boldsymbol{\mathbf{\varepsilon}}} \end{split} \end{equation} \]
Combined Spatial Autocorrelation Model (SAC)
\[ \begin{equation} \begin{split} {\boldsymbol{\mathbf{y}}}&=\alpha{\boldsymbol{\mathbf{\iota}}}+\rho{\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{y}}}+{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\beta}}}+ {\boldsymbol{\mathbf{u}}},\\ {\boldsymbol{\mathbf{u}}}&=\lambda{\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{u}}}+{\boldsymbol{\mathbf{\varepsilon}}} \end{split} \end{equation} \]
Note that all of these models assume different data generating processes (DGP) leading to the spatial pattern. Although there are specifications tests, it is generally not possible to let the data decide which one is the true underlying DGP (Cook, Hays, and Franzese 2015; Rüttenauer 2019). However, there might be theoretical reasons to guide the model specification (Cook, Hays, and Franzese 2015).
Just because SAR is probably the most commonly used model does not make it the best choice. In contrast, various studies (Halleck Vega and Elhorst 2015; Rüttenauer 2019; Wimpy, Whitten, and Williams 2021) highlight the advantages of the relative simple SLX model. Moreover, this specification can basically be incorporated in any other statistical method.
A note on missings
Missing values create a problem in spatial data analysis. For instance, in a local spillover model with an average of 10 neighbours, two initial missing values will lead to 20 missing values in the spatially lagged variable. For global spillover models, one initial missing will ‘flow’ through the neighbourhood system until the cutoff point (and create an excess amount of missings).
Depending on the data, units with missings can either be dropped and omitted from the initial weights creation, or we need to impute the data first, e.g. using interpolation or Kriging.
Spatial Regression Models: Example
We can estimate spatial models using spdep or spatialreg. Both packages contain the same functions, but spatial regression models will be made defunct in spdep in future releases, and will only be available in spatialreg.
SAR
Lets estimate a spatial SAR model using the lagsarlm() with contiguity weights. We use median house value as depended variable, and include population density (POPDEN), the percentage of tree cover (canopy_per), and the number of pubs (pubs_count) and our traffic estimates (traffic)
hv_1.sar <- lagsarlm(log(Value) ~ log(POPDEN) + canopy_per + pubs_count + log(traffic),
data = msoa.spdf,
listw = queens.lw,
Durbin = FALSE) # we could here extend to SDM
summary(hv_1.sar)##
## Call:lagsarlm(formula = log(Value) ~ log(POPDEN) + canopy_per + pubs_count +
## log(traffic), data = msoa.spdf, listw = queens.lw, Durbin = FALSE)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.693579 -0.130072 -0.013419 0.112482 0.886657
##
## Type: lag
## Coefficients: (asymptotic standard errors)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.69443135 0.38774059 6.9491 3.677e-12
## log(POPDEN) -0.00957288 0.01039296 -0.9211 0.3570
## canopy_per 0.00425465 0.00097103 4.3816 1.178e-05
## pubs_count 0.00328093 0.00066826 4.9097 9.123e-07
## log(traffic) -0.03015593 0.02262745 -1.3327 0.1826
##
## Rho: 0.81316, LR test value: 806.35, p-value: < 2.22e-16
## Asymptotic standard error: 0.020691
## z-value: 39.3, p-value: < 2.22e-16
## Wald statistic: 1544.5, p-value: < 2.22e-16
##
## Log likelihood: 82.8018 for lag model
## ML residual variance (sigma squared): 0.041622, (sigma: 0.20401)
## Number of observations: 983
## Number of parameters estimated: 7
## AIC: -151.6, (AIC for lm: 652.74)
## LM test for residual autocorrelation
## test value: 42.212, p-value: 8.1888e-11This looks pretty much like a conventional model output, with some additional information: a highly significant hv_1.sar$rho of 0.81 indicates strong positive spatial autocorrelation. In substantive terms, house prices in the focal unit positively influence house prices in neighbouring units, which again influences house prices among the neighbours of these neighbours, and so on.
NOTE: the coefficients of covariates in a SAR model are not marginal or partical effects, because of the spillovers and feedback loops in \(\boldsymbol{\mathbf{y}}\) (see below)!
SEM
SEM models can be estimated using errorsarlm().
hv_1.sem <- errorsarlm(log(Value) ~ log(POPDEN) + canopy_per + pubs_count + traffic,
data = msoa.spdf,
listw = queens.lw,
Durbin = FALSE) # we could here extend to SDEM
summary(hv_1.sem)##
## Call:errorsarlm(formula = log(Value) ~ log(POPDEN) + canopy_per +
## pubs_count + traffic, data = msoa.spdf, listw = queens.lw,
## Durbin = FALSE)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.635674 -0.122842 -0.011174 0.110979 0.740074
##
## Type: error
## Coefficients: (asymptotic standard errors)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.3468e+01 1.1734e-01 114.7837 < 2.2e-16
## log(POPDEN) -9.0743e-02 1.5294e-02 -5.9331 2.973e-09
## canopy_per 6.7372e-03 1.5726e-03 4.2840 1.835e-05
## pubs_count 7.4751e-04 7.8931e-04 0.9470 0.34361
## traffic -4.2456e-06 2.1379e-06 -1.9859 0.04704
##
## Lambda: 0.84845, LR test value: 830.53, p-value: < 2.22e-16
## Asymptotic standard error: 0.018848
## z-value: 45.016, p-value: < 2.22e-16
## Wald statistic: 2026.4, p-value: < 2.22e-16
##
## Log likelihood: 96.73913 for error model
## ML residual variance (sigma squared): 0.039529, (sigma: 0.19882)
## Number of observations: 983
## Number of parameters estimated: 7
## AIC: -179.48, (AIC for lm: 649.05)In this case hv_1.sem$lambda gives us the spatial parameter. A highly significant lambda of 0.85 indicates that the errors are highly spatially correlated (e.g. due to correlated unobservables). In spatial error models, we can interpret the coefficients directly, as in a conventional linear model.
SLX
Above, we could have estimated SDM and SDEM models using the Durbin option. SLX models can either be estimated with lmSLX() directly, or by creating \(\boldsymbol{\mathbf{W}} \boldsymbol{\mathbf{X}}\) manually and plugging it into any available model-fitting function.
hv_1.slx <- lmSLX(log(Value) ~ log(POPDEN) + canopy_per + pubs_count + traffic,
data = msoa.spdf,
listw = queens.lw,
Durbin = TRUE) # use a formula to lag only specific covariates
summary(hv_1.slx)##
## Call:
## lm(formula = formula(paste("y ~ ", paste(colnames(x)[-1], collapse = "+"))),
## data = as.data.frame(x), weights = weights)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.77623 -0.20247 -0.03854 0.16324 1.38886
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.181e+01 1.185e-01 99.623 < 2e-16 ***
## log.POPDEN. -6.089e-02 2.409e-02 -2.528 0.011636 *
## canopy_per 8.620e-03 2.597e-03 3.319 0.000937 ***
## pubs_count 3.488e-03 1.233e-03 2.830 0.004753 **
## traffic 7.080e-07 4.279e-06 0.165 0.868627
## lag.log.POPDEN. 2.807e-01 3.026e-02 9.275 < 2e-16 ***
## lag.canopy_per 9.964e-03 3.414e-03 2.918 0.003601 **
## lag.pubs_count 1.550e-02 1.703e-03 9.099 < 2e-16 ***
## lag.traffic -3.212e-06 4.784e-06 -0.671 0.502111
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.31 on 974 degrees of freedom
## Multiple R-squared: 0.2951, Adjusted R-squared: 0.2893
## F-statistic: 50.97 on 8 and 974 DF, p-value: < 2.2e-16In SLX models, we can simply interpret the coefficients of direct and indirect (spatially lagged) covariates.
For instance, lets look at population density:
A high population density in the focal unit is related to lower house prices, but
A high population density in the neighbouring areas in related to higher house prices (while keeping population density in the focal unit constant).
Potential interpretation: areas with a low population density in central regions of the city (high pop density around) have higher house prices. We could try testing this interpretation by including the distance to the city center as a control.
Another way of estimating the same model is lagging the covariates first.
# Loop through vars and create lagged variables
msoa.spdf$log_POPDEN <- log(msoa.spdf$POPDEN)
vars <- c("Value", "log_POPDEN", "canopy_per", "pubs_count", "traffic")
for(v in vars){
msoa.spdf[, paste0("w.", v)] <- lag.listw(queens.lw,
var = st_drop_geometry(msoa.spdf)[, v])
}
# Alternatively:
w_vars <- create_WX(st_drop_geometry(msoa.spdf[, vars]),
listw = queens.lw,
prefix = "w")
head(w_vars)## w.Value w.log_POPDEN w.canopy_per w.pubs_count w.traffic
## [1,] 843550.0 4.662014 9.201539 37.000000 19913.92
## [2,] 353666.7 3.300901 19.324093 1.333333 32807.77
## [3,] 329000.0 4.009795 15.861733 1.571429 28656.96
## [4,] 337000.0 3.630360 25.492108 1.400000 27086.95
## [5,] 316650.0 3.993660 17.011171 1.000000 26240.78
## [6,] 317375.0 3.876070 23.598908 1.000000 25371.37And subsequently we use those new variables in a linear model.
hv_1.lm <- lm (log(Value) ~ log(POPDEN) + canopy_per + pubs_count + traffic +
w.log_POPDEN + w.canopy_per + w.pubs_count + w.traffic,
data = msoa.spdf)
summary(hv_1.lm)##
## Call:
## lm(formula = log(Value) ~ log(POPDEN) + canopy_per + pubs_count +
## traffic + w.log_POPDEN + w.canopy_per + w.pubs_count + w.traffic,
## data = msoa.spdf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.77623 -0.20247 -0.03854 0.16324 1.38886
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.181e+01 1.185e-01 99.623 < 2e-16 ***
## log(POPDEN) -6.089e-02 2.409e-02 -2.528 0.011636 *
## canopy_per 8.620e-03 2.597e-03 3.319 0.000937 ***
## pubs_count 3.488e-03 1.233e-03 2.830 0.004753 **
## traffic 7.080e-07 4.279e-06 0.165 0.868627
## w.log_POPDEN 2.807e-01 3.026e-02 9.275 < 2e-16 ***
## w.canopy_per 9.964e-03 3.414e-03 2.918 0.003601 **
## w.pubs_count 1.550e-02 1.703e-03 9.099 < 2e-16 ***
## w.traffic -3.212e-06 4.784e-06 -0.671 0.502111
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.31 on 974 degrees of freedom
## Multiple R-squared: 0.2951, Adjusted R-squared: 0.2893
## F-statistic: 50.97 on 8 and 974 DF, p-value: < 2.2e-16Looks pretty similar to lmSLX() results, and it should! A big advantage of the SLX specification is that we can use the lagged variables in basically all methods which take variables as inputs, such as non-linear models, matching algorithms, and machine learning tools.
Moreover, using the lagged variables gives a high degree of freedom. For instance, we could (not saying that it necessarily makes sense):
Use different weights matrices for different variables
Include higher order neighbours using
nblag()(with an increasing number of orders we go towards a more global model, but we estimate a coefficient for each spillover, instead of estimating just one)Use machine learning techniques to determine the best fitting weights specification.
Impacts
Coefficient estimates \(\neq\) `marginal’ effects
Attention: Do not interpret coefficients as marginal effects in SAR, SAC, and SDM!! Using the reduced form
\[ \begin{equation} \begin{split} {\boldsymbol{\mathbf{y}}} & =\alpha{\boldsymbol{\mathbf{\iota}}}+\rho {\boldsymbol{\mathbf{W}}}{\boldsymbol{\mathbf{y}}}+{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\beta}}}+{\boldsymbol{\mathbf{\varepsilon}}} \\ {\boldsymbol{\mathbf{y}}} & =({\boldsymbol{\mathbf{I}}}-\rho{\boldsymbol{\mathbf{W}}})^{-1}(\alpha{\boldsymbol{\mathbf{\iota}}}+{\boldsymbol{\mathbf{X}}}{\boldsymbol{\mathbf{\beta}}}+{\boldsymbol{\mathbf{\varepsilon}}}), \end{split} \end{equation} \]
we can calculate the first derivative:
\[
\begin{equation}
\begin{split}
\frac{\partial \boldsymbol{\mathbf{y}}}{\partial \boldsymbol{\mathbf{x}}_k} & = ({\boldsymbol{\mathbf{I}}}-\rho{\boldsymbol{\mathbf{W}}})^{-1}\beta_k \\
& =({\boldsymbol{\mathbf{I}}} + \rho{\boldsymbol{\mathbf{W}}} + \rho^2{\boldsymbol{\mathbf{W}}}^2 + \rho^3{\boldsymbol{\mathbf{W}}}^3 + ...)\beta_k,
\end{split}
\end{equation}
\]
where \(\rho{\boldsymbol{\mathbf{W}}}\beta_k\) equals the effect stemming from direct neighbours, \(\rho^2{\boldsymbol{\mathbf{W}}}^2\beta_k\) the effect stemming from second order neighbours (neighbours of neighbours),… This also includes feedback loops if unit \(i\) is also a second order neighbour of itself.
Impact measures
Note that the derivative in SAR, SAC, and SDM is a \(N \times N\) matrix, returning individual effects of each unit on each other unit, differentiated in direct, indirect, and total impacts. However, the individual effects (how \(i\) influences \(j\)) mainly vary because of variation in \({\boldsymbol{\mathbf{W}}}\). Usually, one should use summary measures to report effects in spatial models (LeSage and Pace 2009). Halleck Vega and Elhorst (2015) provide a nice summary of the impacts for each model:
| Model | Direct Impacts | Indirect Impacts |
|---|---|---|
| OLS/SEM | \(\beta_k\) | – |
| SAR/SAC | Diagonal elements of \(({\boldsymbol{\mathbf{I}}}-\rho{\boldsymbol{\mathbf{W}}})^{-1}\beta_k\) | Off-diagonal elements of \(({\boldsymbol{\mathbf{I}}}-\rho{\boldsymbol{\mathbf{W}}})^{-1}\beta_k\) |
| SLX/SDEM | \(\beta_k\) | \(\theta_k\) |
| SDM | Diagonal elements of \(({\boldsymbol{\mathbf{I}}}-\rho{\boldsymbol{\mathbf{W}}})^{-1}\left[\beta_k+{\boldsymbol{\mathbf{W}}}\theta_k\right]\) | Off-diagonal elements of \(({\boldsymbol{\mathbf{I}}}-\rho{\boldsymbol{\mathbf{W}}})^{-1}\) |
The different indirect effects / spatial effects mean conceptionally different things:
Global spillover effects: SAR, SAC, SDM
Local spillover effects: SLX, SDEM
We can calculate these impacts using impacts() with simulated distributions, e.g. for the SAR model:
hv_1.sar.imp <- impacts(hv_1.sar, listw = queens.lw, R = 300)
summary(hv_1.sar.imp, zstats = TRUE, short = TRUE)## Impact measures (lag, exact):
## Direct Indirect Total
## log(POPDEN) -0.011961068 -0.03927592 -0.05123699
## canopy_per 0.005316082 0.01745614 0.02277222
## pubs_count 0.004099436 0.01346110 0.01756054
## log(traffic) -0.037679081 -0.12372480 -0.16140388
## ========================================================
## Simulation results ( variance matrix):
## ========================================================
## Simulated standard errors
## Direct Indirect Total
## log(POPDEN) 0.0130102466 0.043768097 0.056655760
## canopy_per 0.0012331039 0.004271136 0.005390426
## pubs_count 0.0008338459 0.003167338 0.003914092
## log(traffic) 0.0309132727 0.103070402 0.133596604
##
## Simulated z-values:
## Direct Indirect Total
## log(POPDEN) -0.8802702 -0.8802595 -0.8821665
## canopy_per 4.2887709 4.1240007 4.2487680
## pubs_count 4.8931675 4.3085647 4.5289756
## log(traffic) -1.1632894 -1.1484917 -1.1552433
##
## Simulated p-values:
## Direct Indirect Total
## log(POPDEN) 0.37871 0.37872 0.37769
## canopy_per 1.7966e-05 3.7235e-05 2.1495e-05
## pubs_count 9.9226e-07 1.6432e-05 5.9270e-06
## log(traffic) 0.24471 0.25077 0.24799# Alternative with traces (better for large W)
W <- as(queens.lw, "CsparseMatrix")
trMatc <- trW(W, type="mult")
hv_1.sar.imp2 <- impacts(hv_1.sar, tr = trMatc, R = 300, Q = 10)
summary(hv_1.sar.imp2, zstats = TRUE, short = TRUE)## Impact measures (lag, trace):
## Direct Indirect Total
## log(POPDEN) -0.011959920 -0.03917357 -0.05113349
## canopy_per 0.005315572 0.01741065 0.02272622
## pubs_count 0.004099043 0.01342602 0.01752507
## log(traffic) -0.037675465 -0.12340237 -0.16107784
## ========================================================
## Simulation results ( variance matrix):
## ========================================================
## Simulated standard errors
## Direct Indirect Total
## log(POPDEN) 0.012718729 0.042704569 0.055250465
## canopy_per 0.001226630 0.004416743 0.005513989
## pubs_count 0.000903274 0.003390950 0.004182196
## log(traffic) 0.029997064 0.099546125 0.129108144
##
## Simulated z-values:
## Direct Indirect Total
## log(POPDEN) -0.9367921 -0.9266381 -0.9318743
## canopy_per 4.2822322 3.9513430 4.1176688
## pubs_count 4.5928834 4.0717818 4.2933998
## log(traffic) -1.2565638 -1.2408680 -1.2486960
##
## Simulated p-values:
## Direct Indirect Total
## log(POPDEN) 0.34887 0.35411 0.35140
## canopy_per 1.8503e-05 7.7714e-05 3.8272e-05
## pubs_count 4.3716e-06 4.6655e-05 1.7596e-05
## log(traffic) 0.20891 0.21465 0.21178The indirect effects in SAR, SAC, and SDM refer to global spillover effects. This means a change of \(x\) in the focal units flows through the entire system of neighbours (direct nieightbours, neighbours of neighbours, …) influencing ‘their \(y\).’ One can think of this as diffusion or a change in a long-term equilibrium.
For SLX models, nothing is gained from computing the impacts.
print(impacts(hv_1.slx, listw = queens.lw))## Impact measures (SlX, estimable):
## Direct Indirect Total
## log(POPDEN) -6.089155e-02 2.806582e-01 2.197667e-01
## canopy_per 8.619994e-03 9.964079e-03 1.858407e-02
## pubs_count 3.488207e-03 1.549554e-02 1.898374e-02
## traffic 7.079975e-07 -3.211922e-06 -2.503925e-06Geographically weighted regression
Does the relation between \(y\) and \(x\) vary depending on the region we are looking at? With geographically weighted regressions (GWR), we can exploit the spatial heterogeneity in relations / coefficients.
GWR (Brunsdon, Fotheringham, and Charlton 1996; Gollini et al. 2015) is mainly an explorative tool for spatial data analysis in which we estimate an equation at different geographical points. For \(L\) given locations across London, we receive \(L\) different coefficients.
\[ \begin{align} \hat{\boldsymbol{\mathbf{\beta}}}_l=& ({\boldsymbol{\mathbf{X}}}^\intercal{\boldsymbol{\mathbf{M}}}_l{\boldsymbol{\mathbf{X}}})^{-1}{\boldsymbol{\mathbf{X}}}^\intercal{\boldsymbol{\mathbf{M}}}_l{\boldsymbol{\mathbf{Y}}}, \end{align} \]
The \(N \times N\) matrix \({\boldsymbol{\mathbf{M}}}_l\) defines the weights at each local point \(l\), assigning higher weights to closer units. The local weights are determined by a kernel density function with a pre-determined bandwidth \(b\) around each point (either a fixed distance or an adaptive k nearest neighbours bandwidth). Models are estimated via gwr.basic() or gwr.robust() of the GWmodel package.
# Search for the optimal bandwidth
set.seed(123)
hv_1.bw <- bw.gwr(log(Value) ~ log(POPDEN) + canopy_per + pubs_count + traffic,
data = as_Spatial(msoa.spdf),
kernel = "boxcar",
adaptive = TRUE) ## Warning in showSRID(SRS_string, format = "PROJ", multiline = "NO", prefer_proj =
## prefer_proj): Discarded datum OSGB 1936 in Proj4 definition
## Warning in showSRID(SRS_string, format = "PROJ", multiline = "NO", prefer_proj =
## prefer_proj): Discarded datum OSGB 1936 in Proj4 definition## Adaptive bandwidth: 615 CV score: 108.7605
## Adaptive bandwidth: 388 CV score: 94.48697
## Adaptive bandwidth: 247 CV score: 83.5383
## Adaptive bandwidth: 160 CV score: 69.65072
## Adaptive bandwidth: 106 CV score: 62.56455
## Adaptive bandwidth: 73 CV score: 57.72322
## Adaptive bandwidth: 52 CV score: 53.30272
## Adaptive bandwidth: 39 CV score: 51.4244
## Adaptive bandwidth: 31 CV score: 48.39134
## Adaptive bandwidth: 26 CV score: 46.89638
## Adaptive bandwidth: 23 CV score: 46.15693
## Adaptive bandwidth: 21 CV score: 46.76553
## Adaptive bandwidth: 24 CV score: 46.5556
## Adaptive bandwidth: 22 CV score: 46.73153
## Adaptive bandwidth: 23 CV score: 46.15693hv_1.bw## [1] 23### GWR
hv_1.gwr <- gwr.robust(log(Value) ~ log(POPDEN) + canopy_per + pubs_count + traffic,
data = as_Spatial(msoa.spdf),
kernel = "boxcar",
adaptive = TRUE,
bw = hv_1.bw,
longlat = FALSE)## Warning in showSRID(SRS_string, format = "PROJ", multiline = "NO", prefer_proj =
## prefer_proj): Discarded datum OSGB 1936 in Proj4 definition## Warning in proj4string(data): CRS object has comment, which is lost in output
## Warning in proj4string(data): CRS object has comment, which is lost in outputprint(hv_1.gwr)## ***********************************************************************
## * Package GWmodel *
## ***********************************************************************
## Program starts at: 2021-06-21 15:57:05
## Call:
## gwr.basic(formula = formula, data = data, bw = bw, kernel = kernel,
## adaptive = adaptive, p = p, theta = theta, longlat = longlat,
## dMat = dMat, F123.test = F123.test, cv = T, W.vect = W.vect)
##
## Dependent (y) variable: Value
## Independent variables: POPDEN canopy_per pubs_count traffic
## Number of data points: 983
## ***********************************************************************
## * Results of Global Regression *
## ***********************************************************************
##
## Call:
## lm(formula = formula, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.52127 -0.22134 -0.05055 0.16089 1.77130
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.241e+01 1.025e-01 121.077 < 2e-16 ***
## log(POPDEN) 1.192e-01 1.710e-02 6.973 5.69e-12 ***
## canopy_per 1.274e-02 1.563e-03 8.151 1.10e-15 ***
## pubs_count 1.116e-02 1.087e-03 10.268 < 2e-16 ***
## traffic -4.075e-06 1.213e-06 -3.360 0.000811 ***
##
## ---Significance stars
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Residual standard error: 0.3354 on 978 degrees of freedom
## Multiple R-squared: 0.1711
## Adjusted R-squared: 0.1677
## F-statistic: 50.48 on 4 and 978 DF, p-value: < 2.2e-16
## ***Extra Diagnostic information
## Residual sum of squares: 110.0355
## Sigma(hat): 0.3349129
## AIC: 649.0534
## AICc: 649.1394
## BIC: -263.2593
## ***********************************************************************
## * Results of Geographically Weighted Regression *
## ***********************************************************************
##
## *********************Model calibration information*********************
## Kernel function: boxcar
## Adaptive bandwidth: 23 (number of nearest neighbours)
## Regression points: the same locations as observations are used.
## Distance metric: Euclidean distance metric is used.
##
## ****************Summary of GWR coefficient estimates:******************
## Min. 1st Qu. Median 3rd Qu. Max.
## Intercept 8.5424e+00 1.2514e+01 1.3285e+01 1.4452e+01 18.2880
## log(POPDEN) -8.1927e-01 -2.4736e-01 -9.7021e-02 1.9108e-02 0.5160
## canopy_per -1.2612e-01 -2.9350e-03 6.4943e-03 1.8769e-02 0.1394
## pubs_count -8.9826e-02 -1.0365e-02 -3.6112e-04 7.8650e-03 0.0656
## traffic -1.1478e-04 -1.4860e-05 -2.6279e-06 1.2341e-05 0.0002
## ************************Diagnostic information*************************
## Number of data points: 983
## Effective number of parameters (2trace(S) - trace(S'S)): 185.4244
## Effective degrees of freedom (n-2trace(S) + trace(S'S)): 797.5756
## AICc (GWR book, Fotheringham, et al. 2002, p. 61, eq 2.33): -187.4801
## AIC (GWR book, Fotheringham, et al. 2002,GWR p. 96, eq. 4.22): -462.7414
## BIC (GWR book, Fotheringham, et al. 2002,GWR p. 61, eq. 2.34): -353.479
## Residual sum of squares: 29.76571
## R-square value: 0.7757808
## Adjusted R-square value: 0.7235878
##
## ***********************************************************************
## Program stops at: 2021-06-21 15:57:20The results give a range of coefficients for different locations. Let’s map those individual coefficients.
# Spatial object
gwr.spdf <- st_as_sf(hv_1.gwr$SDF)
gwr.spdf <- st_make_valid(gwr.spdf)
# Map
tmap_mode("view")## tmap mode set to interactive viewingmp2 <- tm_shape(gwr.spdf) +
tm_fill(col = "canopy_per",
style = "hclust", n = 8,
title = "Coefficient",
palette = inferno(n = 8, direction = 1),
legend.hist = TRUE) +
tm_borders(col = "black", lwd = 1) +
tm_layout(legend.frame = TRUE, legend.bg.color = TRUE,
#legend.position = c("right", "bottom"),
legend.outside = TRUE,
main.title = "Coefficient of tree cover",
main.title.position = "center",
title.snap.to.legend = TRUE)
mp2